Çizgi bir üçgen midir? Bu soru oldukça basit gözüken bir sorudur fakat değişik açıdan bakıldığında çok entersan şeyler karşımıza çıkabilir. Üçgen denilen geometrik şekil üç kenarlı olmalıdır fakat buna karşın çizgide kenar yoktur, sadece bir tane çizgi vardır. Üçgenin iç açıları toplamı 180’dir fakat buna karşın çizgide açıdan bahsedilemez, dolayısıyla bu sorunun cevabı ilk bakışta hayır olur. Şimdi farkı bir bakış açısından bakalım.
Bu soruya bir de üçgen olma şartlarından biri olan iki kenarın toplamının diğer kenardan büyük olma şartı üzerinden yaklaşalım. Bu şartın ispatını yapmak için ihtiyacımız olan 2 adet peşpeşe yerleştirilmiş çizgiler ile başlayalım.
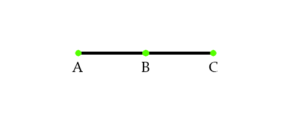
Yukarıda gözüktüğü gibi |AB| ve |BC| birer kenardır. Bu şeklin bir üçgen olabilmesi için bir kenar daha eklenmesi gerekir. Bu kenar |AC| şeklinde eklenebilir fakat bu sefer görünüşte çizgi olarak kalır, üçgen olmaz. Dolayısıyla C noktası B noktasının çevresinde belirli bir derece döndürülmesi gerekir. Ve bu derece ne olursa olsun 0’dan büyük olacağından çizilebilecek |AC| kenarının uzunluğunu kısaltmış olur.
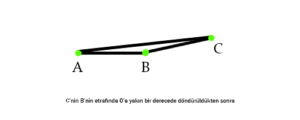
Bu döndürme işlemi üçgen oluşturmak için şarttır. Bu işlemin sonucunda A’dan C’ye bir kenar çizilebilir ve üçgen tamamlanabilir. Burada önemli olan döndürülme işleminden sonra |AB| ve |BC| kenarlarının aynı uzunlukta kalmış olmaları ve C noktasının A’ya biraz da olsa yaklaşmış olmasıdır. Bunun sonucunda |AC| kenarı, |AB| ve |BC| kenarlarının uzunluklarının toplamından kısa olmak zorundadır.
Şimdi sorumuza dönecek olursak, ilk başta kullandığımız A, B ve C noktalarından oluşan 2 kenarlı çizgi bir üçgen sayılabilir mi? Çizgimizde 2 gibi gözükse de aslında 3 kenar bulunur. Bunlar: |AB|, |BC| ve |AC|’dir. |AC| kenarı diğer iki kenarın üstündedir ve bu kapalı bir şekil oluşturur. Dolayısıyla üçgen olmanın ilk şartı olan 3 kenarlı şekil oluşmuş olur. İkinci şart ise iç açılarının toplamının 180 olmasıdır. Çizgiye bakacak olursak A noktasının açısı 0’dır çünkü bağlantısı olan diğer noktalar B ve C aynı hizadadır. B ve C noktalarından biri(C) diğer noktaya(B) A’ya olduğundan daha yakın konumda olduğundan dolayı A açısı 0’dır. C noktasının da bu bakımdan A’dan farkı yoktur ve açısı 0’dır. B’ye gelecek olursak, B aynı hizada olan iki noktanın arasındadır ve bu noktalardan hiçbiri herhangi birine B’ye olduğundan daha yakın konumlanmamıştır dolayısıyla B’nin açısı 180’dir. İkinci şart da bu şekilde sağlanabilir. Üçüncü şart ise bu işe çözüm getirmekte ve çizgi ile üçgenin farkını ortaya koymaktadır. Üçüncü şart ise az önce ispatını yaptığımız herhangi iki kenarın diğer kenardan daha uzun olma şartıdır. Bu şart dolayısıyla üç nokta aynı hizada konumlanamaz çünkü bir kenar her zaman diğer iki kenarın uzunlukları toplamına eşit olur. Bu nedenle çizgiden ayırt edilebilen bir şekil ortaya çıkmaz. Dolayısıyla çizgi bir üçgen değildir.




